class - 11th chapter - 5 NOTES COMPLEX NUMBER

 NOTES  OF COMPLEX NUMBER

Class 11 Maths Notes Chapter 5 Complex Numbers and Quadratic Equations

Imaginary Numbers
The square root of a negative real number is called an imaginary number, e.g. √-2, √-5 etc.
The quantity √-1 is an imaginary unit and it is denoted by ‘i’ called Iota.

Integral Power of IOTA (i)
i = √-1, i2 = -1, i3 = -i, i4 = 1
So, i4n+1 = i, i4n+2 = -1, i4n+3 = -i, i4n = 1

Note:

• For any two real numbers a and b, the result √a × √b : √ab is true only, when atleast one of the given numbers i.e. either zero or positive.
  √-a × √-b ≠ √ab
  So, i2 = √-1 × √-1 ≠ 1
• ‘i’ is neither positive, zero nor negative.
• in + in+1 + in+2 + in+3 = 0

Complex Number
A number of the form x + iy, where x and y are real numbers, is called a complex number, x is called real part and y is called imaginary part of the complex number i.e. Re(Z) = x and Im(Z) = y.

Purely Real and Purely Imaginary Complex Number
A complex number Z = x + iy is a purely real if its imaginary part is 0, i.e. Im(z) = 0 and purely imaginary if its real part is 0 i.e. Re (z) = 0.

Equality of Complex Number
Two complex numbers z1 = x1 + iy1 and z2 = x2 + iy2 are equal, iff x1 = x2 and y1 = y2 i.e. Re(z1) = Re(z2) and Im(z1) = Im(z2)
Note: Order relation “greater than’’ and “less than” are not defined for complex number.

Algebra of Complex Numbers
Addition of complex numbers
Let z1 = x1 + iy1 and z2 = x2 + iy2 be any two complex numbers, then their sum defined as
z1 + z2 = (x1 + iy1) + (x2 + iy2) = (x1 + x2) + i (y1 + y2)

Properties of Addition

• Commutative: z1 + z2 = z2 + z1
• Associative: z1 + (z2 + z3) = (z1 + z2) + z3
• Additive identity z + 0 = z = 0 + z
  Here, 0 is additive identity.

Subtraction of complex numbers
Let z1 = (x1 + iy1) and z2 = (x2 + iy2) be any two complex numbers, then their difference is defined as
z1 – z2 = (x1 + iy1) – (x2 + iy2) = (x1 – x2) + i(y1 – y2)

Multiplication of complex numbers
Let z1 = (x1 + iy1) and z2 = (x2 + iy2) be any two complex numbers, then their multiplication is defined as
z1z2 = (x1 + iy1) (x2 + iy2) = (x1x2 – y1y2) + i (x1y2 + x2y1)

Properties of Multiplication

• Commutative: z1z2 = z2z1
• Associative: z1(z2z3) = (z1z2)z3
• Multiplicative identity: z . 1 = z = 1 . z
  Here, 1 is multiplicative identity of an element z.
• Multiplicative inverse: For every non-zero complex number z, there exists a complex number z1 such that z . z1 = 1 = z1 . z
• Distributive law: z1(z2 + z3) = z1z2 + z1z3

Division of Complex Numbers
Let z1 = x1 + iy1 and z2 = x2 + iy2 be any two complex numbers, then their division is defined as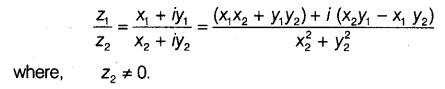

Conjugate of Complex Number
Let z = x + iy, if ‘i’ is replaced by (-i), then said to be conjugate of the complex number z and it is denoted by z¯, i.e. z¯ = x – iy

Properties of Conjugate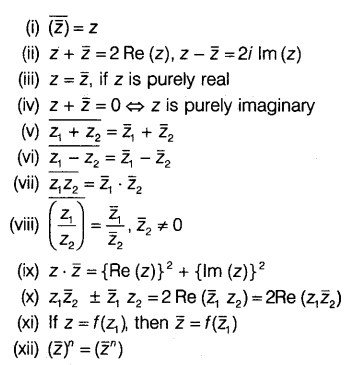

Modulus of a Complex Number
Let z = x + iy be a complex number. Then, the positive square root of the sum of square of real part and square of imaginary part is called modulus (absolute values) of z and it is denoted by |z| i.e. |z| = x2+y2−−−−−−√
It represents a distance of z from origin in the set of complex number c, the order relation is not defined
i.e. z1 > z2 or z1 < z2 has no meaning but |z1| > |z2| or |z1|<|z2| has got its meaning, since |z1| and |z2| are real numbers.

Properties of Modulus of a Complex number

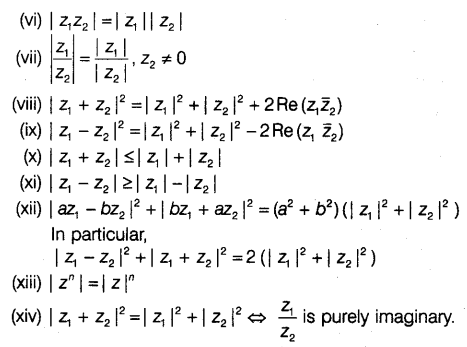
SOLUTIONS OF CH -5

https://www.learncbse.in/ncert-solutions-for-class-11th-maths-chapter-5-complex-numbers-and-quadratic-equations/